JJMMM (III)

Op hoeveel manieren kun je twee jongens in volgorde zetten met drie meisjes? In JJMMM (I) en (II) zagen we dat op 10 manieren kan:

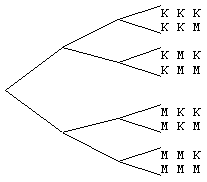
JJMMM  00111

JMJMM  01011

JMMJM  01101

JMMMJ  01110

MJJMM  10011

MJMJM  10101

MJMMJ  10110

MMJJM  11001

MMJMJ  11010

MMMJJ  11100

Vraag is of we die 10 kunnen uitrekenen zonder ze alle tien uit te schrijven.
Ja, dat kan! Wel een heel verhaal.

Stel dat we 5 leerlingen A B C D en E (Anton, Bernard, Cornelia, Daphne en Esther) willen laten plaats nemen op 5 stoelen. Op hoeveel manieren kan dat?

Laten we die stoelen eens op een rij zetten en nummeren van 1 t/m 5.
Voor stoelnummer 1 zijn er 5 kandidaten, voor stoelnummer 2 dan nog slechts 4 kandidaten.
Voor de eerste twee stoelen zijn er dan al 20 mogelijkheden:
AB AC AD AE
BA BC BD BE
CA CB CD CE
DA DB DC DE
EA EB EC ED
Je zou dit mooi in een boomdiagram kunnen zetten, waarbij je eenvoudig ziet dat de eerste twee vertakkingen al 5 x 4 = 20 mogelijkheden opleveren, maar zonder boom moet het ook lukken toch? Belangrijk is dat je begrijpt dat je 5 KEER 4 moet doen, en niet bijvoorbeeld 5 plus 4, of 5 tot de macht 4, of 5 keer 5...

Voor stoelnummer 3 zijn er nog 3 kandidaten over. Voor de eerste drie stoelen heb je dus al 20 x 3 = 60 mogelijkheden. Je raadt het al, voor de eerste vier stoelen heb je dus 5 x 4 x 3 x 2 = 120 volgordes en voor 5 stoelen dus 5 x 4 x 3 x 2 x 1 = 120 volgordes. Voor de laatste stoel blijft er immers 1 leerling over. Een totaal van 120 volgordes dus, te veel om uit te schrijven.

Als je dit lastig vindt, probeer het dan eerst eens met minder leerlingen.
2 leerlingen kunnen op 2 manieren plaats nemen op 2 stoelen: XY en YX
3 leerlingen kunnen op 6 manieren plaatsnemen op 3 stoelen: XYZ XZY YXZ YZX ZXY ZYX
4 leerlingen kunnen op 24 manieren plaatsnemen op 4 stoelen. Je hebt immers keus uit 4 nieuwe kandidaten voor stoel nummer 1, waarbij de overige drie stoelen op 6 manieren bezet kunnen worden. Het totaal aantal manieren voor 4 leerlingen op 4 stoelen is dus 4*6 = 4*(3*2*1) = 24 manieren. 5 leerlingen kunnen dan op 5*24= 5*(4*3*2*1)= 120 manieren plaatsnemen.
Ik hoop dat je het begrijpt.

Op je rekenmachine zit een knopje x met een uitroepteken. Daarmee kun je snel 5 x 4 x 3 x 2 x 1 uitrekenen: 5 x 4 x 3 x 2 x 1 noteer je als 5! (spreek uit: 5 faculteit). Je rekenmachine geeft 120.
Maar hoe bereken je hiermee op hoeveel manieren je twee jongens en drie meisjes in volgorde kunt zetten? We zijn er bijna, nog even geduld!

Stel dat de jongens Anton (A) en Bernard (B) op stoelnummers 1 en 2 plaatsnemen en de drie meisjes Cornelia (C), Daphne (D) en Esther (E) op de overige stoelen, bijvoorbeeld als volgt:
ABCDE dan is dat dus een voorbeeld van JJMMM
Maar als A en B onderlinge wisselen, dan heb je nog steeds JJMMM, met andere woorden:
als je alleen maar op het geslacht let, en niet op de naam, dan verschilt ABCDE niet van BACDE.
Ook de meisjes kunnen onderling van stoel wisselen zonder dat er iets verandert aan JJMMM
Laat ik alle mogelijkheden met JJMMM eens opschrijven.
ABCDE   BACDE
ABCED   BACED
ABDCE   BADCE
ABDEC   BADEC
ABECD   BAECD
ABEDC   BAEDC
Dat zijn er dus twaalf. Ofwel van de 120 volgordes waarop 5 leerlingen A B C D E kunnen plaatsnemen, zijn er twaalf met JJMMM

Maar ook als de jongens helemaal rechts zitten en de meisjes links (MMMJJ), dan zijn daar er twaalf van, en om en om (MJMJM) kan ook op 12 manieren. Het maakt eigenlijk niet uit, overal waar twee jongens en drie meisjes plaatsnemen, daar zijn er twaalf van. Met andere woorden: die 120 moet je delen door twaalf om het aantal volgordes met twee jongens en drie meisje te berekenen.

Samenvattend.
Op hoeveel manieren kunnen twee jongens en drie meisjes plaatsnemen als je alleen op het geslacht let? Antwoord: op 5!/(2!*3!) = 120/ (2*6) = 120/12 = 10 manieren.
5! omdat 5 leerlingen ABCDE op 5*4*3*2*1= 120 manieren kunnen plaatsnemen
Delen door 2! omdat de twee jongens op 2*1 = 2 manieren onderling kunnen wisselen zonder dat het geslacht verandert. Ook delen door 3! omdat drie meisjes steeds onderling op 3*2*1 = 6 manieren kunnen wisselen zonder dat het geslacht verandert.

Op de rekenmachine is voor deze berekening een apart knopje beschikbaar: nCr
Als je intypt 5 nCr 2 (ofwel 5C2) dan geeft je rekenmachine direct het juiste aantal volgordes met twee jongens en drie meisjes, namelijk 10. Uiteraard geeft 5C3 hetzelfde antwoord 10, denk daar maar eens over na!

Nog een voorbeeld.
Hoeveel gezinssamenstellingen van vier kinderen zijn er met twee jongens en 2 meisjes?
Antwoord: 4C2 = 4!/(2!*2!)= 24/(2*2)= 24/4=6  Kijk maar
JJMM   MJJM
JMJM   MJMJ
JMMJ   MMJJ
Vier leerlingen A B C en D kunnen op 4*3*2*1 = 24 manieren plaatsnemen op vier stoelen.
Delen door 2! = 2 omdat de jongens steeds kunnen wisselen zonder dat daarbij het geslacht verandert. Nog een keer delen door 2! = 2 omdat ook de twee meisjes kunnen wisselen zonder dat daarbij het geslacht verandert.

JJMMM (II)

De kans op twee jongens en drie meisjes in een willekeurig gezin met vijf kinderen (J/M = 50/50) is 10 op de 32. In JJMMM (I) heb ik het uitgelegd. Het totaal aantal gezinssamenstellingen met vijf kinderen kun je makkelijk uitrekenen met 2⁵ = 32. Maar hoe vind je nu die 10 zonder ze alle 32 uit te schrijven? Dat doen we natuurlijk systematisch, zodat je weer zeker weet dat je niets vergeet en niets dubbel doet. De volgorde van het boomdiagram is wat mij betreft het meest veilig. Als we afspreken dat we langs de takken omhoog steeds jongen nemen en langs de takken omlaag meisje, dan is het eerste gezin met 2 jongens en 3 meisjes:
JJMMM
Meer volgordes met twee jongens voorop zijn er niet.

Dan gaan we nu JM voorop zetten. Let op: niet eerst MJ want in het boomdiagram staat JM... hoger dan MJ... (ga maar na!). Met JM voorop zijn er 3 mogelijkheden:
JMJMM
JMMJM
JMMMJ
De eerste met  JM voorop is JMJMM. Ga na dat JMJMM hoger in de boom staat dan JMMJM en JMMMJ. De tweede (blauw gemarkeerde) jongen kan dus op precies drie plekken bij de andere twee meisjes geplaatst worden. Meer mogelijkheden met JM voorop zijn er niet.

Met MJ voorop zijn er ook drie, kijk maar:
MJJMM
MJMJM
MJMMJ
Meer mogelijkheden met MJ voorop zijn er niet.

Ten slotte kun je nog MM voorop zetten:

MMJJM
MMJMJ
MMMJJ
Merk op dat bij de laatste MMMJJ de jongens helemaal achteraan staan, terwijl ze vooraan begonnen.

Ik zet ze nog allemaal even op een rij. Je ziet dat als je het op deze manier aanpakt, ze inderdaad van 'klein naar groot' gesorteerd staan en dat je ze dus zeker allemaal precies één keer hebt.

JJMMM  00111

JMJMM  01011

JMMJM  01101

JMMMJ  01110

MJJMM  10011

MJMJM  10101

MJMMJ  10110

MMJJM  11001

MMJMJ  11010

MMMJJ  11100

Een volgende keer leg ik uit hoe je die 10 kunt uitrekenen zonder ze alle tien te hoeven uitschrijven. 

JJMMM (I)

Wat is de kans dat je in een willekeurig gezin met 5 kinderen twee jongens aantreft en drie meisjes?

Als jongens en meisjes evenveel kans hebben om geboren te worden, dan kun je hier goed de kansdefinitie van Laplace gebruiken: kans = gunstig/totaal.

Laten we alle mogelijke gezinssamenstellingen met vijf kinderen eens uitschrijven

JJJJJ  00000

JJJJM  00001

JJJMJ  00010

JJJMM  00011

JJMJJ  00100

JJMJM  00101

JJMMJ  00110

JJMMM  00111

JMJJJ  01000

JMJJM  01001

JMJMJ  01010

JMJMM  01011

JMMJJ  01100

JMMJM  01101

JMMMJ  01110

JMMMM  01111

MJJJJ  10000

MJJJM  10001

MJJMJ  10010

MJJMM  10011

MJMJJ  10100

MJMJM  10101

MJMMJ  10110

MJMMM  10111

MMJJJ  11000

MMJJM  11001

MMJMJ  11010

MMJMM  11011

MMMJJ  11100

MMMJM  11101

MMMMJ  11110

MMMMM  11111

Dat zijn er in totaal dus 32. Hoe schrijf je deze nou snel op zonder er eentje te vergeten, of eentje dubbel te doen? Hoe weet je dat het er 32 moeten worden? Als je begrijpt hoe binair tellen werkt, dan zie je dat als je de 0 vervangt door een J en de 1 vervangt door een M, dat alle volgordes netjes gesorteerd staan, van klein naar groot (zie de binaire getallen 00000 t/m 11111 ernaast).
Als iemand je vraagt: noem alle positieve gehele getallen onder de honderd eens op, dan doe je dat ook volgens een bepaald systeem. Ik zou het van klein naar groot doen: 1 2 3 .... 99 en niet alles door elkaar, dat is niet handig! Hetzelfde geldt voor alle gezinssamenstellingen met vijf kinderen, dat doe je niet door elkaar, maar in een handige volgorde. De volgorde die ik wil aanraden is die van het boomdiagram.

Het krijgen van kinderen is eigenlijk niet veel anders dan het werpen met munten :-)
Doe je consequent in het boomdiagram langs de tak omhoog kop en de tak omlaag munt, dan staan alle mogelijkheden met drie munten aan de uiteinden netjes in de goede volgorde:
KKK KKM KMK KMM MKK MKM MMK MMM
Voor 000 001 010 011 100 101 110 111 en JJJ JJM JMJ JMM MJJ MJM MMJ MMM is dat niet anders. Nu we de volgorde van het boomdiagram begrijpen, wil ik als tip nog meegeven hoe je 'copy en paste' kunt gebruiken om alle volgordes met 5 kinderen snel op te schrijven. Laten we klein beginnen.

Hoeveel manieren zijn er om 1 kind te krijgen?  Twee natuurlijk, het wordt een jongen of een meisje.

Hoeveel gezinssamenstellingen zijn er met 2 kinderen? Vier, namelijk JJ, JM, MJ en MM
(let op: JM en MJ is niet hetzelfde want er is er één de oudste en één de jongste)

En met drie kinderen? Nou dat zijn dezelfde vier met twee kinderen aangevuld met een jongen voorop, of dezelfde vier met een meisje voorop. In totaal dus acht.

JJJ  MJJ

JJM  MJM

JMJ  MMJ

JMM  MMM

Met vier kinderen heb je weer dubbel zoveel mogelijkheden, namelijk de acht van net met een jongen voorop, en dezelfde acht met een meisje voorop. Kortom, 16 gezinssamenstellingen met vier kinderen. Om ze alle 16 op te schrijven zou je goed copy paste kunnen gebruiken!

Met vijf kinderen heb je dus 2x2x2x2x2 = 2⁵ = 32 mogelijkheden
Slechts 10 daarvan bevatten 2 jongens en drie meisjes. Ik heb ze hierboven in het roze gemarkeerd.
De kans dat je in een willekeurig gezin met vijf kinderen 2 jongens en 3 meisjes aantreft is dus 10 op de 32 ofwel 31,25 % kans. Let wel dat de kans op jongen/meisje dan steeds fifty/fifty moet zijn.

Over hoe je die 10 volgordes kunt vinden zonder ze alle 32 uit te schrijven een volgende keer meer.

Twaalf vierkeuzevragen

Ach, we doen het alleen bij het proefwerk statistiek in klas 2: twaalf vierkeuzevragen. Behalve makkelijk nakijken kan ik slechts één ander voordeel noemen van een meerkeuzetoets, namelijk eraan rekenen bij het hoofdstuk kans.
Ik klas 2 beperken we ons tot de kansdefinitie van Laplace: kans is gunstig/totaal
Voorwaarde hierbij is wel dat alle mogelijkheden evenveel kans hebben.

Voor de twaalf vierkeuzevragen uit het proefwerk statistiek, steeds met antwoorden A B C of D, geldt dat je deze op 4¹² = 16777216 verschillende manieren kunt invullen.
Als je die puur op de gok invult, dan heb je dus slechts 1 op de 16 a 17 miljoen kans dat je alles goed gokt. Niet erg groot dus.

Je kan op 3¹² = 531441 manieren alle vragen fout gokken. Dat lijkt enorm, maar op de 16777216 is dat slechts een kans van 3,2 %.

Op hoeveel manieren kun je precies 1 van de 12 vragen goed invullen (en dus ook 11 fout)? Bijvoorbeeld GFFF FFFF FFFF.  Nou, dat kan op 1*3¹¹ = 177147 manieren.
Maar vraagnummer 2 had ook goed kunnen zijn: FGFF FFFF FFFF. Daar zijn er ook 177147 van.
In totaal zijn er dus 12*1*3¹¹ = 2125764 manieren om precies 1 van de 12 vragen goed te doen. Dat is meer dan alles fout. De kans op precies 1 van de 12 goed is:
p(1 v/d 12 G) = 12*1*3¹¹/4¹²  = 0,127 = 12,7%

De kans op 2 van de 12 vragen is nog groter namelijk:
p(2 v/d 12 G) =  66*1²*3¹⁰/4¹²  = 0,232 = 23,2%
Die 66 kun je als volgt beredeneren.
GGFF FFFF FFFF Met de blauwe G voorop kan de rode G op 11 posities staan.
FGGF FFFF FFFF  Met de blauwe G op positie 2 kan de rode G nog slechts op 10 plekken staan.
FFGG FFFF FFFF  Met de blauwe G op positie 3 kan de rode G nog slechts op 9 plekken staan.
In totaal zijn er 11+10+9+8+7+6+5+4+3+2+1= 66 volgordes met 2 keer een G en 10 keer een F.
In een vorige les heb ik de leerlingen geleerd dat je dit ook kan uitrekenen met faculteiten en met nCr. Voor 2 goed en 10 fout bereken je 66 met 12!/(2!*10!) of nog sneller met 12C2.

Zodoende konden we vrij vlot onderstaande tabel vullen:

Je ziet dat de kans op 0 tot en met 7 van de 12 goed samen al 99,7% is en dat de kans op drie van de twaalf goed het grootst is, namelijk 25,8 %. Nogal wiedes, je verwacht bij vierkeuzevragen uiteraard dat je een kwart van de vragen sowieso goed gokt. De kans op 3 goed moet dan wel het grootst zijn. Bij 3 van de twaalf goed vinden wij dat het proefwerkcijfer één hoort. De overige negen vragen zijn dan 1 punt per stuk waard, dus 12 goed wordt een tien, 11 goed een negen, 10 goed een acht, 9 goed en zeven, 8 goed een zes, etc.
De kans op een voldoende (minstens 8 goed) als je de test puur op de gok invult is dus slechts 0,3%. Het loont dus om dit proefwerk goed voor te bereiden:-)

Proefwerk statistiek is overigens goed gemaakt, kans moet nog komen, maar dan alleen met vragen waarvan je alle mogelijkheden kunt uitschrijven, nCr is voor klas 4.

Test1

Het is alweer $9+\frac{9}{\sqrt{9}}$ uur geweest.

$\sqrt{3x-1}+(1+x)^2$


$P(E) = {n \choose k} p^k (1-p)^{ n-k}$


$\frac{1}{\Bigl(\sqrt{\phi \sqrt{5}}-\phi\Bigr) e^{\frac25 \pi}} = 1+\frac{e^{-2\pi}} {1+\frac{e^{-4\pi}} {1+\frac{e^{-6\pi}} {1+\frac{e^{-8\pi}} {1+\ldots} } } }$

Op Wisplan vind je extra digitaal lesmateriaal. Ga naar www.wisplan.nl voor meer informatie.